C Programing !!! Solution:- #include<stdio.h> #include<conio.h> void main(){ int akshay,bhavik,dhansree; clrscr(); printf("Enter ages of Akshay,Bhavik,Dhanshree"); scanf("%d %d %d",&akshay,&bhavik,&dhanshree); if(akshay<bhavik) { if(akshay<dhanshree) printf("Akshay is Younger"); else printf("Dhanshree is Younger"); } else { if(bhavik<dhanshree) printf("Bhavik is Younger"); else printf("Dhanshree is Younger"); } getch(); }
Popular posts from this blog
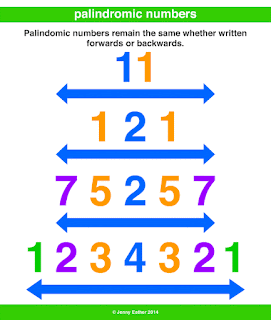
Palindromic Number
PALINDROMIC NUMBER A palindromic number or numeral palindrome is a number that remains the same when its digits are reversed. Like 16461, for example, it is "symmetrical". The term palindromic is derived from palindrome, which refers to a word (such as rotor or racecar) whose spelling is unchanged when its letters are reversed. The first 30 palindromic numbers (in decimal) are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, … and so on Although palindromic numbers are most often considered in the decimal system, the concept of palindromicity can be applied to the natural numbers in any numeral system . Consider a number n > 0 in base b ≥ 2, where it is written in standard notation with k +1 digits a i as: {...
Prime Number
PRIME NUMBER A prime number is a whole number greater than 1 whose only factors are 1 and itself. A factor is a whole numbers that can be divided evenly into another number. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29. Numbers that have more than two factors are called composite numbers. The number 1 is neither prime nor composite. For every prime number p , there exists a prime number p ' such that p ' is greater than p . This mathematical proof, which was demonstrated in ancient times by the Greek mathematician Euclid, validates the concept that there is no "largest" prime number. As the set of natural numbers N = {1, 2, 3, ...} proceeds, however, prime numbers generally become less frequent and are more difficult to find in a reasonable amount of time. As of this writing, the largest known prime number has more than 23 million digits. It is referred to as M77232917 and...



Comments
Post a Comment