DataCode

ENGLISH ALPHABETS  Program to Display English Alphabets #include <stdio.h> int main () { char c ; for ( c = 'A' ; c <= 'Z' ; ++ c ) printf ( "%c " , c ); return 0 ; } Output: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

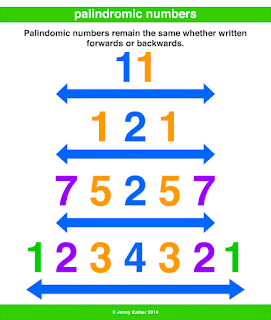
PALINDROMIC NUMBER  A palindromic number or numeral palindrome is a number that remains the same   when its digits are reversed. Like 16461, for example, it is "symmetrical".  The term palindromic is derived from palindrome, which refers to a word  (such as rotor or racecar) whose spelling is unchanged when its letters are reversed. The first 30 palindromic numbers (in decimal) are:  0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161,   171, 181, 191, 202, … and so on  Although palindromic numbers are most often considered in the decimal  system,   the concept   of  palindromicity  can be applied to the natural numbers  in any   numeral system . Consider a   number  n  > 0 in base   b  ≥ 2, where it is written in   standard notation with  k +1 digits   a i  as: {\displaystyle n=\sum _{i=0}^{k}a_{i}b^{i}}  with, as usual, 0 ≤  a i  <  b  for all  i  and  a k  ≠ 0. Then  n  is palindromic if and only   if 

FIBONACCI SERIES: The Fibonacci Series is an infinite sequence of integers. like; 0, 1, 1, 2, 3, 5, 8, 13 and so on........ The first two integers 0 and 1 are initial values. The Nth Fibonacci Number where N >2 is the sum of two immediate preceding two elements. The recursive definition to find nth Fibonacci number is given by,  The C function to find the nth Fibonacci number using recursive definition is shown in example 1. The way to find fib(4) is shown in figure 1. The thick arrows represent either a call to function  fib()  or to the value. The dashed arrows point to the result after computation. The iterative technique for this much more efficient than the recursive technique. C PROGRAM TO DISPLAY FIBONACCI SERIES /* Fibonacci series program in C language */ #include <stdio.h> int   main ( ) {     int   n ,   first   =   0 ,   second   =   1 ,   next ,   c ;     printf ( "Enter the number of terms \n " ) ;    

Solution :- #include<stdio.h> #include<conio.h> void main(){ float km,m,feet,inch,cm; printf("Enter the distance between two cities(in km) - "); scanf("%f",&km); m = km*1000; //since 1km = 1000m feet= km*3280.84; //since 1km=3280.84feet inch=km*39370.1; //since 1 km=39370.1inches cm=km*100000; //since 1km = 100000cm printf("\nDistance in kilometres = %f ",km); printf("\nDistance in metres = %f ",m); printf("\nDistance in feet = %f ",feet); printf("\nDistance in inches = %f ",inch); printf("\nDistance in centimetres = %f ",cm); getch(); }