Palindromic Number

PALINDROMIC NUMBER

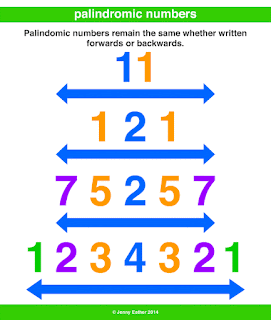
 A palindromic number or numeral palindrome is a number that remains the same   when its digits are reversed. Like 16461, for example, it is "symmetrical". 

The term palindromic is derived from palindrome, which refers to a word 

(such as rotor or racecar) whose spelling is unchanged when its letters are reversed.The first 30 palindromic numbers (in decimal) are:

 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161,   171, 181, 191, 202, … and so on

 Although palindromic numbers are most often considered in the decimal system,   the concept   of palindromicity can be applied to the natural numbers in any   numeral system. Consider a   number n > 0 in base b ≥ 2, where it is written in   standard notation with k+1 digits a_i as:

${\displaystyle n=\sum _{i=0}^{k}a_{i}b^{i}}$

 with, as usual, 0 ≤ a_i < b for all i and a_k ≠ 0. Then n is palindromic if and only   if a_i = a_k−i for   all i. zero is written 0 in any base and is also palindromic by   definition.

C Program to Check Whether a Number is Palindrome or Not

This program reverses an integer (entered by the user) using while loop. Then, if statement is used to check whether the reversed number is equal to the original number or not.

#include <stdio.h>
int main()
{
    int n, reversedInteger = 0, remainder, originalInteger;

    printf("Enter an integer: ");
    scanf("%d", &n);

    originalInteger = n;

    // reversed integer is stored in variable 
    while( n!=0 )
    {
        remainder = n%10;
        reversedInteger = reversedInteger*10 + remainder;
        n /= 10;
    }

    // palindrome if orignalInteger and reversedInteger are equal
    if (originalInteger == reversedInteger)
        printf("%d is a palindrome.", originalInteger);
    else
        printf("%d is not a palindrome.", originalInteger);
    
    return 0;
}

Output:

Enter an integer: 2002
2002 is a palindrome.